Algorithms
You can find all the definitions here in the book "Introduction to graph theory", Douglas.B West. Important graph algorithms :
While running DFS, we assign colors to the vertices (initially white). Algorithm itself is really simple :
Time complexity : O(n + m).
Lemma: If we run dfs(root) in a rooted tree, then v is an ancestor of u if and only if stv ≤ stu ≤ ftu ≤ ftv .
So, given arrays st and ft we can rebuild the tree.
Problems: 500D - New Year Santa Network, 475B - Strongly Connected City
Code :
Time complexity : O(n + m).
In this algorithm, first of all we run DFS on the graph and sort the vertices in decreasing of their finishing time (we can use a stack).
Then, we start from the vertex with the greatest finishing time, and for each vertex v that is not yet in any SCC, do : for each u that v is reachable by u and u is not yet in any SCC, put it in the SCC of vertex v. The code is quite simple.
Problems: CAPCITY, BOTTOM
Pseudo code :
One) O(n2)
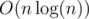
1) Using
It is too simple and undrestandable :
The main idea is to relax all the edges exactly n - 1 times (read relaxation above in dijkstra). You can prove this algorithm using induction.
If in the n - th step, we relax an edge, then we have a negative cycle (this is if and only if).
Code :
The origin of this algorithm is unknown. It's said that at first Chinese coders used it in programming contests.
Its code looks like the combination of Dijkstra and BFS :
Best MST algorithms :
Then in order of the sorted array, we add ech edge if and only if after adding it there won't be any cycle (check it using DSU).
Code :
.
where weight(i, j) is the weight of the edge from i to j) .
So, pseudo code will be like this:
One) O(n2)
I only wanna put the source code here (EdmondsKarp):
Input: A network G = ((V, E), c, s, t).
Output: A max s - t flow.
.
Theorem: Maximum flow = minimum cut.
Add two vertices S, T to the graph, every edge from X to Y (graph parts) has capacity 1, add an edge from S with capacity 1 to every vertex in X, add an edge from every vertex in Y with capacity 1 to T.
Finally, answer = maximum matching from S to T .
But it can be done really easier using DFS.
As, you know, a bipartite matching is the maximum matching if and only if there is no augmenting path (read Introduction to graph theory).
The code below finds a augmenting path:
Problem: 498C - Array and Operations
In the last lectures we talked about segment trees on trees and heavy-light decomposition.
Example: Having a rooted tree, each vertex has a value (initially 0), each query gives you numbers v and u (v is an ancestor of u) and asks you to increase the value of all vertices in the path from u to v by 1.
So, we have an array p, and for each query, we increase p[u] by 1 and decrease p[par[v]] by 1. The we run this (like a normal partial sum):
For example, in each node, we have a vector, all nodes in its subtree (this can be used only for offline queries, because we may have to delete it for memory usage).
Here again we use DSU technique, we will have a vector V for every node. When we want to have V[v] we should merge the vectors of its children. I mean if its children are u1, u2, ..., uk where V[u1].size() ≤ V[u2].size() ≤ ... ≤ V[uk].size(), we will put all elements from V[ui] for every 1 ≤ i < k, in V[k] and then, V[v] = V[uk].
Using this trick, time complexity will be.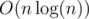
C++ example (it's a little complicated) :
There are so many algorithms for this, I will discuss the important ones.
Each algorithm has complexities < O(f(n)), O(g(n)) > , it means that this algorithm's preprocess is O(f(n)) and answering a query is O(g(n)) .
In all algorithms, h[v] = height of vertex v.
One) Brute force < O(n), O(n) >
The simplest approach. We go up enough to achieve the goal.
Preproccess :
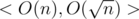
I talked about SQRT decomposition in the first lecture.
Here, we will cut the tree into
(H = height of the tree), starting from 0, k - th of them contains all vertices with h in interval 
.
Also, for each vertex v in k - th piece, we store r[v] that is, its lowest ancestor in the piece number k - 1.
Preprocess:
Let's introduce you an order of tree vertices, haas and I named it Euler order. It is like DFS order, but every time we enter a vertex, we write it's number down (even when we come from a child to this node in DFS).
Code for calculate this :
For this propose we can use RMQ problem, and the best algorithm for that, is to use Sparse table.
Four) Something like Sparse table :)
This is the most useful and simple (among fast algorithms) algorithm.
For each vector v and number i, we store its 2i-th ancestor. This can be done in.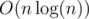
Then, for each query, we find the lowest ancestors of them which are in
the same height, but different (read the source code for
understanding).
Preprocess:
DFS
The most useful graph algorithms are search algorithms. DFS (Depth First Search) is one of them.While running DFS, we assign colors to the vertices (initially white). Algorithm itself is really simple :
dfs (v):
color[v] = gray
for u in adj[v]:
if color[u] == white
then dfs(u)
color[v] = blackTime complexity : O(n + m).
DFS tree
DFS tree is a rooted tree that is built like this :let T be a new tree
dfs (v):
color[v] = gray
for u in adj[v]:
if color[u] == white
then dfs(u) and par[u] = v (in T)
color[v] = blackStarting time, finishing time
Starting time of a vertex is the time we enter it (the order we enter it) and its finishing time is the time we leave it. Calculating these are easy :TIME = 0
dfs (v):
st[v] = TIME ++
color[v] = gray
for u in adj[v]:
if color[u] == white
then dfs(u)
color[v] = black
ft[v] = TIME // or we can use TIME ++Lemma: If we run dfs(root) in a rooted tree, then v is an ancestor of u if and only if stv ≤ stu ≤ ftu ≤ ftv .
So, given arrays st and ft we can rebuild the tree.
Finding cut edges
The code below works properly because the lemma above (first lemma):h[root] = 0
par[v] = -1
dfs (v):
d[v] = h[v]
color[v] = gray
for u in adj[v]:
if color[u] == white
then par[u] = v and dfs(u) and d[v] = min(d[v], d[u])
if d[u] > h[v]
then the edge v-u is a cut edge
else if u != par[v])
then d[v] = min(d[v], h[u])
color[v] = blackFinding cut vertices
The code below works properly because the lemma above (first lemma):h[root] = 0
par[v] = -1
dfs (v):
d[v] = h[v]
color[v] = gray
for u in adj[v]:
if color[u] == white
then par[u] = v and dfs(u) and d[v] = min(d[v], d[u])
if d[u] >= h[v] and (v != root or number_of_children(v) > 1)
then the edge v is a cut vertex
else if u != par[v])
then d[v] = min(d[v], h[u])
color[v] = blackFinding Eulerian tours
It is quite like DFS, with a little change :vector E
dfs (v):
color[v] = gray
for u in adj[v]:
erase the edge v-u and dfs(u)
color[v] = black
push v at the end of eProblems: 500D - New Year Santa Network, 475B - Strongly Connected City
BFS
BFS is another search algorithm (Breadth First Search). It is usually used to calculate the distances from a vertex v to all other vertices in unweighted graphs.Code :
BFS(v):
for each vertex i
do d[i] = inf
d[v] = 0
queue q
q.push(v)
while q is not empty
u = q.front()
q.pop()
for each w in adj[u]
if d[w] == inf
then d[w] = d[u] + 1, q.push(w)Time complexity : O(n + m).
BFS tree
BFS tree is a rooted tree that is built like this :let T be a new tree
BFS(v):
for each vertex i
do d[i] = inf
d[v] = 0
queue q
q.push(v)
while q is not empty
u = q.front()
q.pop()
for each w in adj[u]
if d[w] == inf
then d[w] = d[u] + 1, q.push(w) and par[w] = u (in T)SCC
The most useful and fast-coding algorithm for finding SCCs is Kosaraju.In this algorithm, first of all we run DFS on the graph and sort the vertices in decreasing of their finishing time (we can use a stack).
Then, we start from the vertex with the greatest finishing time, and for each vertex v that is not yet in any SCC, do : for each u that v is reachable by u and u is not yet in any SCC, put it in the SCC of vertex v. The code is quite simple.
Problems: CAPCITY, BOTTOM
Shortest path
Shortest path algorithms are algorithms to find some shortest paths in directed or undirected graphs.Dijkstra
This algorithm is a single source shortest path (from one source to any other vertices). Pay attention that you can't have edges with negative weight.Pseudo code :
dijkstra(v) :
d[i] = inf for each vertex i
d[v] = 0
s = new empty set
while s.size() < n
x = inf
u = -1
for each i in V-s //V is the set of vertices
if x >= d[i]
then x = d[i], u = i
insert u into s
// The process from now is called Relaxing
for each i in adj[u]
d[i] = min(d[i], d[u] + w(u,i))
One) O(n2)
int mark[MAXN];
void dijkstra(int v){
fill(d,d + n, inf);
fill(mark, mark + n, false);
d[v] = 0;
int u;
while(true){
int x = inf;
u = -1;
for(int i = 0;i < n;i ++)
if(!mark[i] and x >= d[i])
x = d[i], u = i;
if(u == -1) break;
mark[u] = true;
for(auto p : adj[u]) //adj[v][i] = pair(vertex, weight)
if(d[p.first] > d[u] + p.second)
d[p.first] = d[u] + p.second;
}
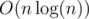
}1) Using
std :: set :void dijkstra(int v){
fill(d,d + n, inf);
d[v] = 0;
int u;
set<pair<int,int> > s;
s.insert({d[v], v});
while(!s.empty()){
u = s.begin() -> second;
s.erase(s.begin());
for(auto p : adj[u]) //adj[v][i] = pair(vertex, weight)
if(d[p.first] > d[u] + p.second){
s.erase({d[p.first], p.first});
d[p.first] = d[u] + p.second;
s.insert({d[p.first], p.first});
}
}
}std :: priority_queue (better):bool mark[MAXN];
void dijkstra(int v){
fill(d,d + n, inf);
fill(mark, mark + n, false);
d[v] = 0;
int u;
priority_queue<pair<int,int>,vector<pair<int,int> >, less<pair<int,int> > > pq;
pq.push({d[v], v});
while(!pq.empty()){
u = pq.top().second;
pq.pop();
if(mark[u])
continue;
mark[u] = true;
for(auto p : adj[u]) //adj[v][i] = pair(vertex, weight)
if(d[p.first] > d[u] + p.second){
d[p.first] = d[u] + p.second;
pq.push({d[p.first], p.first});
}
}
}Floyd-Warshall
Floyd-Warshal algorithm is an all-pairs shortest path algorithm using dynamic programming.It is too simple and undrestandable :
Floyd-Warshal()
d[v][u] = inf for each pair (v,u)
d[v][v] = 0 for each vertex v
for k = 1 to n
for i = 1 to n
for j = 1 to n
d[i][j] = min(d[i][j], d[i][k] + d[k][j])Bellman-Ford
Bellman-Ford is an algorithm for single source shortest path where edges can be negative (but if there is a cycle with negative weight, then this problem will be NP).The main idea is to relax all the edges exactly n - 1 times (read relaxation above in dijkstra). You can prove this algorithm using induction.
If in the n - th step, we relax an edge, then we have a negative cycle (this is if and only if).
Code :
Bellman-Ford(int v)
d[i] = inf for each vertex i
d[v] = 0
for step = 1 to n
for all edges like e
i = e.first // first end
j = e.second // second end
w = e.weight
if d[j] > d[i] + w
if step == n
then return "Negative cycle found"
d[j] = d[i] + w
SPFA
SPFA (Shortest Path Faster Algorithm) is a fast and simple algorithm (single source) that its complexity is not calculated yet. But if m = O(n2) it's better to use the first implementation of Dijkstra.The origin of this algorithm is unknown. It's said that at first Chinese coders used it in programming contests.
Its code looks like the combination of Dijkstra and BFS :
SPFA(v):
d[i] = inf for each vertex i
d[v] = 0
queue q
q.push(v)
while q is not empty
u = q.front()
q.pop()
for each i in adj[u]
if d[i] > d[u] + w(u,i)
then d[i] = d[u] + w(u,i)
if i is not in q
then q.push(i)MST
MST = Minimum Spanning Tree :) (if you don't know what it is, google it).Best MST algorithms :
Kruskal
In this algorithm, first we sort the edges in ascending order of their weight in an array of edges.Then in order of the sorted array, we add ech edge if and only if after adding it there won't be any cycle (check it using DSU).
Code :
Kruskal()
solve all edges in ascending order of their weight in an array e
ans = 0
for i = 1 to m
v = e.first
u = e.second
w = e.weight
if merge(v,u) // there will be no cycle
then ans += wPrim
In this approach, we act like Dijkstra. We have a set of vertices S, in each step we add the nearest vertex to S, in S (distance of v from where weight(i, j) is the weight of the edge from i to j) .So, pseudo code will be like this:
Prim()
S = new empty set
for i = 1 to n
d[i] = inf
while S.size() < n
x = inf
v = -1
for each i in V - S // V is the set of vertices
if x >= d[v]
then x = d[v], v = i
d[v] = 0
S.insert(v)
for each u in adj[v]
do d[u] = min(d[u], w(v,u))One) O(n2)
bool mark[MAXN];
void prim(){
fill(d, d + n, inf);
fill(mark, mark + n, false);
int x,v;
while(true){
x = inf;
v = -1;
for(int i = 0;i < n;i ++)
if(!mark[i] and x >= d[i])
x = d[i], v = i;
if(v == -1)
break;
d[v] = 0;
mark[v] = true;
for(auto p : adj[v]){ //adj[v][i] = pair(vertex, weight)
int u = p.first, w = p.second;
d[u] = min(d[u], w);
}
}
}void prim(){
fill(d, d + n, inf);
set<pair<int,int> > s;
for(int i = 0;i < n;i ++)
s.insert({d[i],i});
int v;
while(!s.empty()){
v = s.begin() -> second;
s.erase(s.begin());
for(auto p : adj[v]){
int u = p.first, w = p.second;
if(d[u] > w){
s.erase({d[u], u});
d[u] = w;
s.insert({d[u], u});
}
}
}
}std :: priority_queue instead of std :: set.Maximum Flow
You can read all about maximum flow here.I only wanna put the source code here (EdmondsKarp):
algorithm EdmondsKarp
input:
C[1..n, 1..n] (Capacity matrix)
E[1..n, 1..?] (Neighbour lists)
s (Source)
t (Sink)
output:
f (Value of maximum flow)
F (A matrix giving a legal flow with the maximum value)
f := 0 (Initial flow is zero)
F := array(1..n, 1..n) (Residual capacity from u to v is C[u,v] - F[u,v])
forever
m, P := BreadthFirstSearch(C, E, s, t, F)
if m = 0
break
f := f + m
(Backtrack search, and write flow)
v := t
while v ≠ s
u := P[v]
F[u,v] := F[u,v] + m
F[v,u] := F[v,u] - m
v := u
return (f, F)
algorithm BreadthFirstSearch
input:
C, E, s, t, F
output:
M[t] (Capacity of path found)
P (Parent table)
P := array(1..n)
for u in 1..n
P[u] := -1
P[s] := -2 (make sure source is not rediscovered)
M := array(1..n) (Capacity of found path to node)
M[s] := ∞
Q := queue()
Q.offer(s)
while Q.size() > 0
u := Q.poll()
for v in E[u]
(If there is available capacity, and v is not seen before in search)
if C[u,v] - F[u,v] > 0 and P[v] = -1
P[v] := u
M[v] := min(M[u], C[u,v] - F[u,v])
if v ≠ t
Q.offer(v)
else
return M[t], P
return 0, P
algorithm EdmondsKarp
input:
graph (Graph with list of Adjacency nodes with capacities,flow,reverse and destinations)
s (Source)
t (Sink)
output:
flow (Value of maximum flow)
flow := 0 (Initial flow to zero)
q := array(1..n) (Initialize q to graph length)
while true
qt := 0 (Variable to iterate over all the corresponding edges for a source)
q[qt++] := s (initialize source array)
pred := array(q.length) (Initialize predecessor List with the graph length)
for qh=0;qh < qt && pred[t] == null
cur := q[qh]
for (graph[cur]) (Iterate over list of Edges)
Edge[] e := graph[cur] (Each edge should be associated with Capacity)
if pred[e.t] == null && e.cap > e.f
pred[e.t] := e
q[qt++] : = e.t
if pred[t] == null
break
int df := MAX VALUE (Initialize to max integer value)
for u = t; u != s; u = pred[u].s
df := min(df, pred[u].cap - pred[u].f)
for u = t; u != s; u = pred[u].s
pred[u].f := pred[u].f + df
pEdge := array(PredEdge)
pEdge := graph[pred[u].t]
pEdge[pred[u].rev].f := pEdge[pred[u].rev].f - df;
flow := flow + df
return flowDinic's algorithm
Here is Dinic's algorithm as you wanted.Input: A network G = ((V, E), c, s, t).
Output: A max s - t flow.
1.set f(e) = 0 for each e in E
2.Construct G_L from G_f of G. if dist(t) == inf, then stop and output f
3.Find a blocking flow fp in G_L
4.Augment flow f by fp and go back to step 2.Theorem: Maximum flow = minimum cut.
Maximum Matching in bipartite graphs
Maximum matching in bipartite graphs is solvable also by maximum flow like below :Add two vertices S, T to the graph, every edge from X to Y (graph parts) has capacity 1, add an edge from S with capacity 1 to every vertex in X, add an edge from every vertex in Y with capacity 1 to T.
Finally, answer = maximum matching from S to T .
But it can be done really easier using DFS.
As, you know, a bipartite matching is the maximum matching if and only if there is no augmenting path (read Introduction to graph theory).
The code below finds a augmenting path:
bool dfs(int v){// v is in X, it reaturns true if and only if there is an augmenting path starting from v
if(mark[v])
return false;
mark[v] = true;
for(auto &u : adj[v])
if(match[u] == -1 or dfs(match[u])) // match[i] = the vertex i is matched with in the current matching, initially -1
return match[v] = u, match[u] = v, true;
return false;
}for(int i = 0;i < n;i ++)if(match[i] == -1){
memset(mark, false, sizeof mark);
dfs(i);
}while(true){
memset(mark, false, sizeof mark);
bool fnd = false;
for(int i = 0;i < n;i ++) if(match[i] == -1 && !mark[i])
fnd |= dfs(i);
if(!fnd)
break;
}Problem: 498C - Array and Operations
Trees
Trees are the most important graphs.In the last lectures we talked about segment trees on trees and heavy-light decomposition.
Partial sum on trees
We can also use partial sum on trees.Example: Having a rooted tree, each vertex has a value (initially 0), each query gives you numbers v and u (v is an ancestor of u) and asks you to increase the value of all vertices in the path from u to v by 1.
So, we have an array p, and for each query, we increase p[u] by 1 and decrease p[par[v]] by 1. The we run this (like a normal partial sum):
void dfs(int v){
for(auto u : adj[v])
if(u - par[v])
dfs(u), p[v] += p[u];
}DSU on trees
We can use DSU on a rooted tree (not tree DSUs, DSUs like vectors).For example, in each node, we have a vector, all nodes in its subtree (this can be used only for offline queries, because we may have to delete it for memory usage).
Here again we use DSU technique, we will have a vector V for every node. When we want to have V[v] we should merge the vectors of its children. I mean if its children are u1, u2, ..., uk where V[u1].size() ≤ V[u2].size() ≤ ... ≤ V[uk].size(), we will put all elements from V[ui] for every 1 ≤ i < k, in V[k] and then, V[v] = V[uk].
Using this trick, time complexity will be
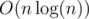.C++ example (it's a little complicated) :
typedef vector<int> vi;
vi *V[MAXN];
void dfs(int v, int par = -1){
int mx = 0, chl = -1;
for(auto u : adj[v])if(par - u){
dfs(u,v);
if(mx < V[u]->size()){
mx = V[u]->size();
chl = u;
}
}
for(auto u : adj[v])if(par - u and chl - u){
for(auto a : *V[u])
V[chl]->push_back(a);
delete V[u];
}
if(chl + 1)
V[v] = V[chl];
else{
V[v] = new vi;
V[v]->push_back(v);
}
}LCA
LCA of two vertices in a rooted tree, is their lowest common ancestor.There are so many algorithms for this, I will discuss the important ones.
Each algorithm has complexities < O(f(n)), O(g(n)) > , it means that this algorithm's preprocess is O(f(n)) and answering a query is O(g(n)) .
In all algorithms, h[v] = height of vertex v.
One) Brute force < O(n), O(n) >
The simplest approach. We go up enough to achieve the goal.
Preproccess :
void dfs(int v,int p = -1){
if(par + 1)
h[v] = h[p] + 1;
par[v] = p;
for(auto u : adj[v]) if(p - u)
dfs(u,v);
}int LCA(int v,int u){
if(v == u)
return v;
if(h[v] < h[u])
swap(v,u);
return LCA(par[v], u);
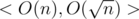
}I talked about SQRT decomposition in the first lecture.
Here, we will cut the tree into
(H = height of the tree), starting from 0, k - th of them contains all vertices with h in interval .Also, for each vertex v in k - th piece, we store r[v] that is, its lowest ancestor in the piece number k - 1.
Preprocess:
void dfs(int v,int p = -1){
if(par + 1)
h[v] = h[p] + 1;
par[v] = p;
if(h[v] % SQRT == 0)
r[v] = p;
else
r[v] = r[p];
for(auto u : adj[v]) if(p - u)
dfs(u,v);
}int LCA(int v,int u){
if(v == u)
return v;
if(h[v] < h[u])
swap(v,u);
if(h[v] == h[u])
return (r[v] == r[u] ? LCA(par[v], par[u]) : LCA(r[v], r[u]));
if(h[v] - h[u] < SQRT)
return LCA(par[v], u);
return LCA(r[v], u);
}Let's introduce you an order of tree vertices, haas and I named it Euler order. It is like DFS order, but every time we enter a vertex, we write it's number down (even when we come from a child to this node in DFS).
Code for calculate this :
vector<int> euler;
void dfs(int v,int p = -1){
euler.push_back(v);
for(auto u : adj[v]) if(p - u)
dfs(u,v), euler.push_back(v);
}vector<pair<int,int> > instead of this and push {h[v], v} in the vector, and the first time {h[v], v} is appeared is s[v] and s[v] < s[u] then LCA(v, u) = (mini = s[v]s[u]euler[i]).second.For this propose we can use RMQ problem, and the best algorithm for that, is to use Sparse table.
Four) Something like Sparse table :)
This is the most useful and simple (among fast algorithms) algorithm.
For each vector v and number i, we store its 2i-th ancestor. This can be done in
.
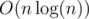Then, for each query, we find the lowest ancestors of them which are in
the same height, but different (read the source code for
understanding).Preprocess:
int par[MAXN][MAXLOG]; // initially all -1
void dfs(int v,int p = -1){
par[v][0] = p;
if(p + 1)
h[v] = h[p] + 1;
for(int i = 1;i < MAXLOG;i ++)
if(par[v][i-1] + 1)
par[v][i] = par[par[v][i-1]][i-1];
for(auto u : adj[v]) if(p - u)
dfs(u,v);
}
Comments
Post a Comment